
Summary
angle(h,v): the argument (angle), in radians, of vector (h,v).
sinh(a); cosh(a); tanh(a) are the hyperbolic functions. The
inverses (a...) are available but do not work yet.
a^b: Raise a to power b. Use sqrt(a) instead of a^0.5
for square root.
ln(t); log(t,b)
r(c,x',y'); g(c,x',y'); b(c,x',y'): Inter-referencing. The
possibilities of these functions are infinite and exposed in chapter three.
c is a project number, it must be a constant. (x',y') is the
coordinate that will be read.
Operators priority is %; +; -; *; /; ^. When having the same operator several
times, the left-most one has more priority. Example: a/b^2/c is read as
a/((b^2)/c), which equals to "ac÷b²". This is not as we
usually read them. Take care!
Angle(h,v)
This function takes an horizontal distance as first argument and a vertical one
as second argument.
It returns a number between -pi and pi and some undefined value when both
arguments are zero.
I have found two important uses to this function.
The actual reason why I created this function was for spirals.
You calculate the sine of the sum of the angle and the distance. You get the
angle with angle(dx,dy) and the distance with sqrt(dx^2+dy^2)
Try the following equation and try to change the constants in it:
| sin(angle(x-128,y-128)+sqrt((x-128)^2+(y-128)^2)/3)*127+128 |  |
If you replace
the power of two by power of a larger even number (eg ten), you'll notice that
your spiral gets square (you also have to adjust the other numerical constants
for that).
If you multiply the angle() function in the above equation by a whole number,
you will get more than one spiral on the same picture (actually as many as the
number you multiplied by)
If you add a constant somewhere inside the sine function, it will make your
spiral turn. If you multiply or divide the distance by some constant, you can
set the distance between two rings of the spiral.
Note that instead
of putting the angle() function on its own, you can put some function of it, you
can do polar graphics.
For instance take its sine (having multiplied it by a sufficiently large
number). You would get a picture like this:
If you want to have only one ring, then use an implicit function.
The other main
use of the angle function is precisely for implicit functions.
If you want to get only the results of the equation on some area of the picture,
then you can use an arctangent of the angle function, maybe having first taken
its absolute value.
More on this in the implicit function chapter.
sinh(), cosh(),
tanh() are hyperbolic functions. Their actual meaning will probably never be of
any use for picFX, so I won't explain it here. (Well, shortly, it's the same as
trigonometric function sin cos tan, except that we are not moving on a circle
but on the right branch an hyperbola)
Their mathematical definition is sinh(z)=½(e^z-e^(-z)), cosh(z)=½(e^z+e^(-z))
and tanh=sinh/cosh.
What is important to see here is the exponentials e^... They cause the cosh and
sinh functions to take really big values once the argument is a bit large.
sinh(x) has similar properties as x^3, ie it has the same sign as x and sinh(0)
equals 0, and sinh(-x)=-sinh(x) (ie the graph is symmetric through the center).
cosh(x) is roughly equal to abs(sinh(x)), except that cosh(0) equals one, ie
cosh is always bigger than one.
The physicians
would tell you that the hyperbolic cosine is the equation of the chain, ie you
hold a chain between your two hands, and the curve, looking like a parabolic but
*not* a parabolic is a hyperbolic cosine :-)
Well, this interesting feature has no use in picFX, unless you want to draw
realistic strings or chains in your picture [but remember then to take care of
the perspective] ;-)
I use sinh and cosh very rarely. It is possible to replace a square somewhere by an hyperbolic cosine, just for fun...(But remember that cosh(x) is always bigger or equal to one, while x^2 goes down to zero!)
tanh, however, is always between -1 and 1, and can replace very handfully arctangent, as you do not have to divide by pi every time you use it :-)
(You can think of arctangent as being roughly equal to the sign of x (-1 or +1) but with a smooth change near zero...)
Mmh. Well.
You have a headache?
Shall I dear to speak about the ^ (power) operator before we go to easy stuff again? :-)
You know, the main reason why I created picFX was just to have fun, and I invite you to have fun as well... If you feel tired just write anything in the fields (I mean, anything but still mathematical :-) and look what comes, then try to transform it a little until it reaches to something nice...
...
Welcome again ;-)
a^b, as said
above, is a to the power of b. Usually you will have b constant, eg for
calculating the square of some value (eg for the famous Pythagoras theorem, when
calculating the distance between two points).
When working in floating point mode, you can have b fractional. Note that a
negative number raised to a fractional power is not defined as a real number and
therefore returns some random value in picFX
Raising a
variable to a large even number is gives near of (but superior to) zero when
between -1 and +1, gives one on these two bounds and yields very large values
out of this [-1,1] range.
If you do something like adding one and doing the inverse, you will get about
one between -1 and +1, and about zero elsewhere.
(Then you can multiply an expression by this to put everything out of this strip
to zero...)
This picture shows this function when using 20 as exponent: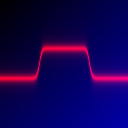
And raising to an uneven number is the same except that the value is negative when the variable is negative.
sqrt(z) is equivalent to z^0.5 but is faster and more accurate (and works in 32bits mode)
ln(z), log(z,b)
are the inverse functions of the exponential.
For instance, log(y,10) is the inverse of x^10, which means that log(y,10)=x is
equivalent to x^10=y. For instance, log(1000,10) is three (as 10^3=1000)...
(b is the base. log(z,b) being for z the inverse of b^x; ln(z) is equal to
log(z,e)).
b must be positive and different from one...
· ln(z) is not
defined (in real numbers) when z is smaller or equal to zero.
· ln(z) is equal to zero when z equals one, and runs towards minus infinity
when z gets near of zero, and slowly grows when z gets a little larger.
· On this picture, you see the graph of the function, horizontal is the value
you give to z and vertical is the value of the logarithm: 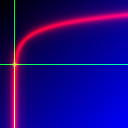 .
.
2.1: Four operators
2.2:
Trigonometric functions
2.3: Min, Max, Modulo, Abs and Neg
2.4: Other functions
3.1: Monochrome graphs
3.2: Implicit functions
3.3: Playing with hyperbolic tangents