Note that
trigonometric functions require a floating point mode
All trigonometric functions in picFX use radient angles. I invite you to forget
about degrees. I have to say you that, except to tell the coordinates on the
earth (or in astronomy) as longitude and latitude (decl/r.-a.), I do never use
degrees at school, for personal research or whatever else. Never.
In radient, the "right" angle (is it so we say? I mean the one between
two perpendicular lines, 90°) is pi/2, the flat angle (=180°) is pi, and the
full angle (=360°) is 2*pi.
When you draw a part (an arc) of a circle (radius 1), the length of the path is
equal to the angle between the two bounds, from the center. And, of course, the
length of the circumference of a circle of radius one is... 2pi.
If you don't know what sin, cos, tan, asin, acos or atan mean...
Imagine an object moving in circle, for example the Moon around the Earth, or
the Earth around the Sun.
Trigonometric functions allow us to know at which coordinate the object is at a
given time. If the circle has a radius of one, the horizontal coordinate is
cos(a), a being the angle the object has moved since being on the right, equal
to the length of the path it made. sin(a) is the vertical coordinate.
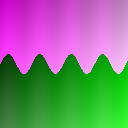
As you can guess, these functions both vary between -1 and 1. To see how the
function looks like, put "y+sin(x/10)*10-128" in a function
field and render.

If you draw a
vertical line tangent to the circle on the right, and then imagine there
is a light in the center of the circle, then tan(a) gives the vertical
coordinate of the "shadow" of the turning object, the crossing point
of the tangent and a line coming from the center and going throught the moving
point.
tan(ąpi/2) is undefined (infinite) because at this moment the
"shadow" does not reach the tangent, and the line going through the
point is vertical and therefore parralel to the tangent..
Note that when the point is on the left half (cos(a)<0), the shadow does not
actually reach the tangent. You are forced to use the line going through the
point and the center :-)
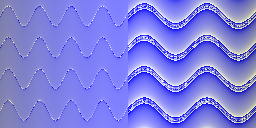
See the appearance of the tangent curve using y+tan(x/10)*10-128, or 25500/((y+tan(x/20)*20-128)^2+100).
acos() is the inverse function of cos(). You give the horizontal coordinate and
you get the angle. Obviously, acos(x) is not defined if x is bigger than one or
smaller than -1...
asin() is the inverse of sin().
atan() is the inverse of tan(). This function is defined for any value. You say
where is the "shadow" and you get the angle... It always returns a
value between -pi/2 and +pi/2, with most of the change around zero..
End of definitions :-)
As sin and cos return a value between -1 and 1, it is often (when your
expression is the (co)sine of something and nothing else) needed to multiply it
(127), and add a constant (128) to make it take the [0;255] range. So use
sin(...)*127+128.
Use the sine if you want to have height lines of some function, a line each 2pi,
starting at pi/2. For example, sqrt((x-128)^2+(y-128)^2) (try it!, maybe
putting "255-" at the beginning) is a kind of cone centered on
(128;128), and the sine of it makes concentrical circles...

sin(x/2)*127+128
makes vertical lines; you can think of x/2 to be a little slope raising in your
direction to the right...
The other most handful use of the sine is to make waves. Do two dimensional
waves with sin(x)*sin(y). You can also use addition, but note that it will
return something within [-2;2] instead of [-1;1]...
Do not hesitate to put sines inside sines. Try for example sin(y/2+10*sin(x/10))*127+128

The cosine
function is basically the same as the sine, only with a little (pi/2) shift to
the left.
Tangent. I use this if I want to have some regular areas separated by thin lines
where sudden and chaotic changes occur. Try for example the above one, where you
add a tangent of the horizontal coordinate (and divided the sinx by two, too): sin(tan(x/17)+y/4+5*sin(x/10))*127+128
Also try this tangent of the vertical coordinate to which I added the sine of
the horizontal: tan(y/10+sin(x/5))*2+128. A little variation: tan(y/10+sin(x/10))*40+128
Because of their
annoying limitation to the [-1;1] range, the asin and acos function are not
really useful. (Actually asin(2) and other are defined but not real... wait
picFX version supporting complex numbers :-)
ArcTangent, however can be quite useful if you want a quite sudden colour
change, however smooth. Try atan((y-128)/8)/pi*255+128
A general formula would be: atan(f(x,y))/pi*255+128: dark when f(x,y) is
negative and bright when f(x,y) is positive. The change occur when f(x,y) is
around zero.
This actually shows the solutions of an inequation..
I will come again on this when speaking of implicit functions.
Remember that it outputs a value between -pi/2 and pi/2...
If you feel ready, you can already try to experiment all sorts of functions
using trig. functions, you can get really nice pictures just with the three sin,
tan, atan functions.
As a rule: Do not be afraid to write things that you would think stupid ;-).
(Btw, Divisions by zero, arc[co-]sines on undefined values do not make picFX
crash :-)
2.1:
Four operators
2.2: Trigonometric Functions
2.3: Min, Max,
Modulo, Abs
2.4: Other
functions