 tanh(z) is near of -1 when z is small, and near of +1 when z is large.
tanh(z) is near of -1 when z is small, and near of +1 when z is large.I already defined tanh in section 2.4, but I can say it again :-)
tanh(z) = sinh(z)/cosh(z) = (ez - e-z)/(ez + e-z).
 tanh(z) is near of -1 when z is small, and near of +1 when z is large.
tanh(z) is near of -1 when z is small, and near of +1 when z is large.
And finally, like for sines and cosines, it is always between -1 and +1.
This means that if you want a tanh to be between 0 and 255, you will do
tanh(...)*127+128, like for sines. You will have light in the areas where
the argument is positive, and dark elsewhere.
Okay, maybe you wonder why I find that bunch of exponential interesting enough to devote a whole section to it?
First important use is for displaying the solutions of an inequation.
An inequation is an expression of the form a<0 or
a>0. For instance, x^2+y^2-1<0 is the set
of points inside the circle of radius one:

| r=g=b=tanh((x^2+y^2-1)*3)*127+128 |
So, to view the solutions of an inequation, you will write something like
tanh(f(x))*127+128, where f(x) is the left-hand side of the inequation.
If its value changes quickly from negative to positive values, the border will
be sharp, and will look blurred if it changes slowly. So if you want to make
the borders sharp, multiply the whole inequation by some big constant.

| 
| 
| r(x,y)=tanh(k*(1-(x^2+y^2+.3*sin(7*angle(x,y)))))*127+128 |
| k=30 | k=3 | k=0.3 |
As tanh(z) looks a bit like z near zero and always remains inside the interval
[-1;1], it can be used to constrain a function between two values.
Example:
| 
|
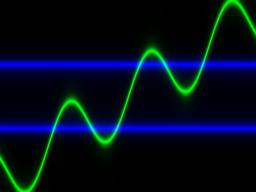
| This is a view of the function sin(x)+x/2 (I showed the solutions
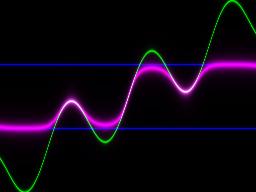
of y=sin(x)+x/2 to obtain this picture), with blue lines at y=+1 and -1: | Now, that one shows, in purple, the same function put inside an hyperbolic
tangent (tanh(sin(x)+x/2)): |
 this picture contains, on the left half, a function that got outside the [0;255],
and that therefore got those holes due to modulo. On the right half is exactely
the same function, but with a tanh applied to it. tanh((...-128)/127)*127+128
keeps the behaviour of "..." between 0 and 255 and makes sure it does not get outside
this interval...
this picture contains, on the left half, a function that got outside the [0;255],
and that therefore got those holes due to modulo. On the right half is exactely
the same function, but with a tanh applied to it. tanh((...-128)/127)*127+128
keeps the behaviour of "..." between 0 and 255 and makes sure it does not get outside
this interval...
You get a funny effect when taking the tanh of a sine multiplied by a large number
(something like tanh(90*sin(x))). As the sine will for most values be
very far of zero, but alternatively with positive and negative values, taking
its hyperbolic tangent will get you a function that switches between -1 and +1.
This picture was obtained doing tanh(30*cos(x*19)) (with x between -0.8 and +0.8),
to which I substracted y and took the tanh (to highlight places where y>tanh(...) and
keep dark other places. I took the opposite for the other colour component.

| tanh((y*17-tanh(30*cos(x*19)))*10)*127+128 |
3.1: Monochrome Graphs
3.2: Implicit functions
3.3: Playing with hyperbolic tangents
4.1: Having fun with colours
4.2: Convolutions
4.3: Linear transformations
Maxime Gamboni Last modified: Sat Jun 23 17:13:47 MET DST 2001